排序算法真的很多,最难受的是你学完以后过了半年就很难很顺利的实现出来了,笔者都已经写过三遍了......,大一时候写了一遍,一年前开始刷题时候学了一遍,面试前还得再看一遍~~,因此本篇博客对排序算法进行了整理,面试前看一下事半功倍。排序算法一般还是结合TOPK手撕,让手写一个快排或者最小堆居多。主要还是排序思想,比如归并排序的分治和。
从稳定和不稳定来看
稳定:冒泡排序、选择排序、归并排序、计数排序、桶排序、基数排序。
不稳定:插入排序、希尔排序、堆排序、快速排序。
从时间复杂度来看,分为平均,最坏,最好。这个应该是很显然的,就是三个层次,O(n^2^)、O(nlogn)、O(n),O(n)只有满足一定条件的非比较排序算法才能满足。
附一个偷的图:
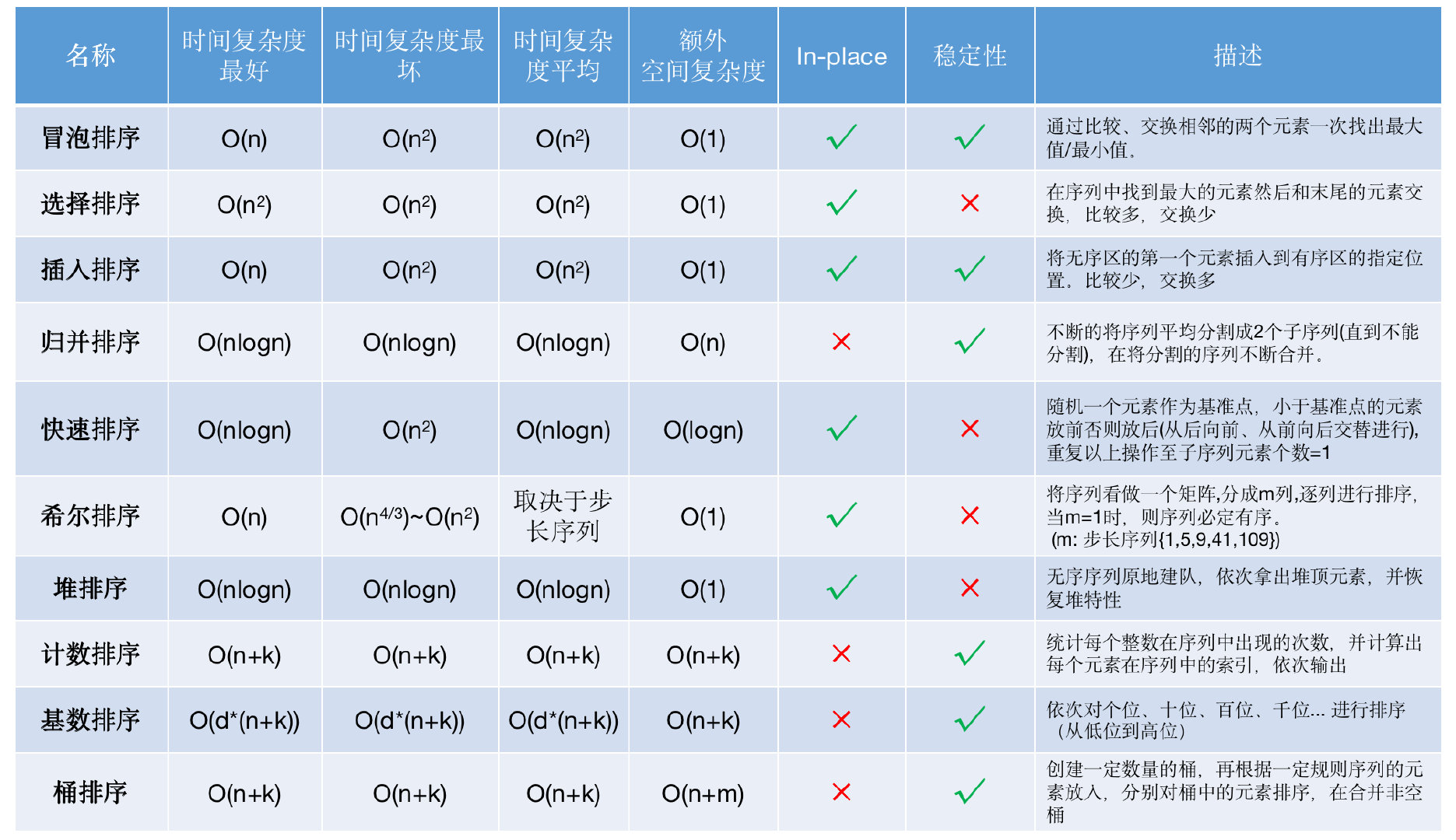
冒泡排序
因为排序过程形似泡泡一个一个往上冒因而得名。特点是相邻元素两两比较,这样最大值或最小值可以浮到数组的最后面。
它的优点是在经过优化后,对于有序或近乎有序的数组可以达到O(n)的时间复杂度。
private void bubbleSort(int[] a) {
int cache = a.length - 1; // 记录后面有序的
int j;
while (true) {
if (cache == 0) return; // 处理到最后一个元素了
j = cache;
for (int i = 0; i < j; i++) {
if (a[i] > a[i + 1]) { // 交换位置
int temp = a[i];
a[i] = a[i + 1];
a[i + 1] = temp;
cache = i;
}
}
}
}选择排序
顾名思义,每轮选择一个最大或最小的元素,然后从前往后目标元素和最大值或最小值交换即可。
优点是简单易懂、移动次数较少、时间复杂度确定
private void selectSort(int[] a) {
for (int i = 0; i < a.length - 1; i++) { // 外层控制排序的元素
int min = i;
for (int j = i + 1; j < a.length; j++) { // 找到剩余元素的最小值
if (a[j] < a[min]) {
min = j;
}
}
if (min != i) {
// 交换元素
int temp = a[i];
a[i] = a[min];
a[min] = temp;
}
}
}堆排序
堆排序是对选择排序的改进,它使用大顶堆来进行内层元素的选择。
优点是时间复杂度改进成了O(nlog(n))。
static class Heap {
int[] arr;
int size = 0;
public Heap(int[] arr) {
this.arr = arr;
this.size = arr.length;
heapify();
}
// 堆化
private void heapify() {
// 弗洛伊德堆化算法
int nonLeafIndex = size / 2 - 1;
for (int i = nonLeafIndex; i >= 0; i--) {
down(i);
}
}
// 取出元素
private int poll() {
if (size == 0) throw new RuntimeException();
int polled = arr[0];
// 首先交换最后一个元素和第一个元素,然后下沉即可。
swap(0, size - 1);
size--;
down(0); // 先size--,再下潜,不然之前删除的那个元素还是会参与比较
return polled;
}
// 下潜
private void down(int parent) {
int left = 2 * parent + 1;
int right = left + 1;
int max = parent;
// 比较left和right哪个值更大
if (left < size && arr[left] > arr[max]) {
max = left;
}
if (right < size && arr[right] > arr[max]) {
max = right;
}
if (max != parent) { // 如果还需要继续下潜的话
swap(max, parent);// 交换两个节点
down(max); // 继续下潜
}
}
private void swap(int curr, int parent) {
int temp = arr[curr];
arr[curr] = arr[parent];
arr[parent] = temp;
}
}
// 堆排序的思想很简单,就是把快排里面找最大值或者最小值的方法用堆实现了,这样可以达到nlog(n)的级别
private void heapSort(int[] a) {
Heap heap = new Heap(a);
for (int i = a.length - 1; i >= 0; i--) {
// 拿到最大值
int max = heap.poll();
a[i] = max; // 直接赋值,不用交换,因为原始值都存到大顶堆里面了
}
}插入排序
插入排序是维护一个有序数组,在未排序数组中取出第一个元素插入到有序数组中,直至未排序数组长度为空。
优点是在小数据量和近乎有序情况下表现优异,常常用来优化编程语言的内置排序函数。
private void insertSort(int[] a) {
for (int i = 1; i < a.length; i++) { // 控制右侧数字
int num = a[i];
int j = i - 1;
// 右移左边数组,直到找到插入位置
while (j >= 0 && a[j] > num) { // 当前元素大于要插入的元素
a[j + 1] = a[j];
j--;
}
if (j != i - 1) { // 寻找完成后判断j是否改变,当然不判断也可以
a[j + 1] = num;
}
}
}希尔排序
希尔排序是对插入排序算法的改进,改变了任意一个元素移动到它应该在的位置的步长,比如可以一次移动32步而非1步。
优点是将插入排序算法的时间复杂度优化到了O(nlog(n))—>O(nlog^2^(n^2^))量级
private void shellSort(int[] a) {
for (int gap = a.length >> 1; gap >= 1; gap/=2) {
// 把之前插入排序的默认1改成gap即可,左边比较的步长也是gap,初始化时候也是gap;
for (int i = gap; i < a.length; i++) {
int num = a[i], j = i - gap;
while (j >= 0 && a[j] > num) {
a[j + gap] = a[j];
j -= gap;
}
if (j != i - gap) {
a[j + gap] = num;
}
}
}
}归并排序
归并排序的思想是分治合,切分到最小可治单元进行合。常常采用递归实现,称为自顶至下实现。
优点是最小、最坏、平均时间复杂度都是O(nlog(n))
private void mergeSort(int[] a) {
split(a, 0, a.length - 1, new int[a.length]);
}
/**
* 切分的递归方法
*
* @param a 原始数组
* @param left 切分的左索引
* @param right 切分的右索引
* @param temp 临时数组,用于合并
*/
private void split(int[] a, int left, int right, int[] temp) {
if (left == right) return; // 切分到只有一个元素了,“治”
// 不停切分,“分”
int mid = (left + right) / 2;
split(a, left, mid, temp);
split(a, mid + 1, right, temp);
// 合并两个有序数组,“合”
merge(a, left, mid, temp, mid + 1, right);
System.arraycopy(temp, left, a, left, right - left + 1); // 从left开始拷贝回去
}
/**
* 合并两个有序数组
*
* @param a 原始数组
* @param l1 数组1左索引
* @param r1 数组1右索引
* @param res 要合并到的数组
* @param l2 数组2左索引
* @param r2 数组2右索引
*/
private void merge(int[] a, int l1, int r1, int[] res, int l2, int r2) {
int p1 = l1, p2 = l2; // 双指针分别指向两个数组的起始索引
int p = l1; // 新数组的索引
// 两个数组元素比较
while (p1 <= r1 && p2 <= r2) {
if (a[p1] <= a[p2]) {
res[p++] = a[p1];
p1++;
} else {
res[p++] = a[p2];
p2++;
}
}
// 处理之前没有处理到的数组
if (p1 != r1 + 1) System.arraycopy(a, p1, res, p, r1 - p1 + 1); // 第一个数组有残留
if (p2 != r2 + 1) System.arraycopy(a, p2, res, p, r2 - p2 + 1); // 第二个数组有残留
}快速排序
快速排序也是采用分治的思想,流程是每轮选择一个基准点,将比它小的元素放到左边,比他大的放到右边,紧接着继续对另外两堆进行处理,直到遍历到每堆是一个元素。
快排的优点是在大数据量情况下几乎是性能最优异的排序算法
快排有两个因为分区十分不均匀导致的缺点
处理反着有序的元素。时间复杂度会达到O(n^2^),使用随机基准点解决
处理大量重复元素,传统分区算法时间复杂度会达到O(n^2^),改写分区算法兼容重复元素
有一个三向切分快速排序,分成三堆可以解决上面提到的两个问题,还是改写的分区算法。
public void quickSort(int[] a) {
quickSort(a, 0, a.length - 1);
}
// 递归入口
private void quickSort(int[] a, int left, int right) {
if (left >= right) return; // left>=right
int idx = partition2(a, left, right);
quickSort(a, left, idx - 1);
quickSort(a, idx + 1, right);
}
// 基础的分区,随机基准点+双边快排
private int partition(int[] a, int left, int right) {
int idx = (int) ((Math.random() * (right - left + 1)) + left); // 生成[left,right]的随机索引
swap(a, left, idx); // 把随机值交换到前面
int pivot = a[left];
int i = left, j = right; // 左右指针,i负责找大于基准点元素的,j负责找小于基准点元素的
// 关于a[j]>pivot还是a[j]>=pivot,这个不影响,因为无论如何这个实现相等元素都会跑到一边去。但是不要都不相等。
while (i < j) {
// 不停找小于等于 基准点元素的
while (i < j && a[j] >= pivot) {
j--;
}
// 不停找大于基准点元素的
while (i < j && a[i] <= pivot) {
i++;
}
swap(a, i, j);
}
swap(a, left, i); // 这个边界条件我的建议是背下来,最后把基准点和i的元素交换
return i;
}
/*
* 改进方法。首先这次左边和右边都是遇到相等的就停下来然后交换。
* 同时更新i和j,这个时候可以把相等的元素打均匀。
* */
private int partition2(int[] a, int left, int right) {
int randomIndex = (int) ((Math.random() * (right - left + 1)) + left); // 生成[left,right]的随机索引
swap(a, randomIndex, left);
int bv = a[left]; // 每次取基准值为当前排序序列的第一个元素
// 使用双边快排实现
int i = left + 1;
int j = right;
// i小于j的时候直接开始找
while (i <= j) {
// 从左往右找,找到第一个比基准值大的元素(这里需要等于)
while (i <= j && a[i] < bv) {
i++;
}
// 从右往左找,使用while循环,直到找到一个比基准值小的或等于的元素
while (i <= j && a[j] > bv) {
j--;
}
// 兜底的判断,用于处理重复元素的情况。这里的两个一个++,一个--
if (i <= j) {
// i和j进行交换
swap(a, i, j);
i++;
j--;
}
}
// 当寻找完毕了,就把基准点换到i或者j这边
swap(a, left, j);
return j;
}
// 交换元素
private void swap(int[] a, int idx1, int idx2) {
int temp = a[idx1];
a[idx1] = a[idx2];
a[idx2] = temp;
}三向切分快速排序
public void quickSort(int[] a) {
quickSort(a, 0, a.length - 1);
}
public static void quickSort(int[] a, int left, int right) {
// 小数据可以使用插入排序,优化性能
if (right - left <= 16) {
insertSort(a, left, right);
return;
}
// 递归出口,注意是left>=right,因为p为0的情况下就会如果相等就会爆栈
if (left >= right) {
return;
}
// 处理逆序数组
int randomIndex = ThreadLocalRandom.current().nextInt(right - left + 1) + left;
swap(a, randomIndex, left);
// 处理重复元素
int lt = left, gt = right; // 声明两个指针
int pivot = a[left]; // 初始化基准点
int i = left; // 初始化指针
// 6 4 3 2 8 5
// i=0 gt=5 pivot=6 i=1 4<6 a[1]=a[0] a[0]=a[1] 4 6 3 2 8 5 i=2
while (i <= gt) {
// 小于基准点的时候更新lt的索引,并且交换原始数组的元素。更新i指针,
// 根据上面的过程可以看到,a[lt]一定是已经判断过了(lt<=i),所以可以更新i指针。
if (a[i] < pivot) {
swap(a, lt++, i++);
// 大于基准点的时候仅仅交换一下位置,不要更新i指针,因为当前交换的元素a[gt]还没有判断呢
} else if (a[i] > pivot) {
swap(a, i, gt--);
}
// 跟基准点相等的元素就直接跳过,不再处理了
else {
i++;
}
}
quickSort(a, left, lt - 1); // 基准点左边的元素
quickSort(a, gt + 1, right); // 基准点右边的元素
}
// 交换元素
private void swap(int[] a, int idx1, int idx2) {
int temp = a[idx1];
a[idx1] = a[idx2];
a[idx2] = temp;
}
